先日家の納戸を整理していたところ、子育てをしていたころの玩具が数点出てきました。
その中にあまり記憶にもなく一見「これは何?」と思えるものがありました。市販の物ではない手作り感満載のものですが、その玩具の意味や目的を知って「なるほど!」と思えるものだったので紹介させていただきます。
見つけたものは、以下の画像の物です。
一辺が8㎝ほどの立方体で、6面のうち5面は表面保護のためか型崩れ防止のためにフィルムが張られています。
サイコロのようにも思えましたが、1~6の数字に相当するものはなく、各面に赤い正方形と青い正方形、そして黒の長方形が描かれています。

これって何の玩具? どうやって遊ぶの?

表面の模様の意味は?
と、少し不思議な思いを抱きました。

何だろう? と思いながら触っていると、フィルムの張られていない面が蓋になっていて開くことに気づきました。そこで開けてみると、中には下の画像のように、これまた手作り感満載の小さな積み木のような木片が入っていました。


積み木の木片以外に、もう一点、以下画像の小さな説明書きの紙片も入っていました。
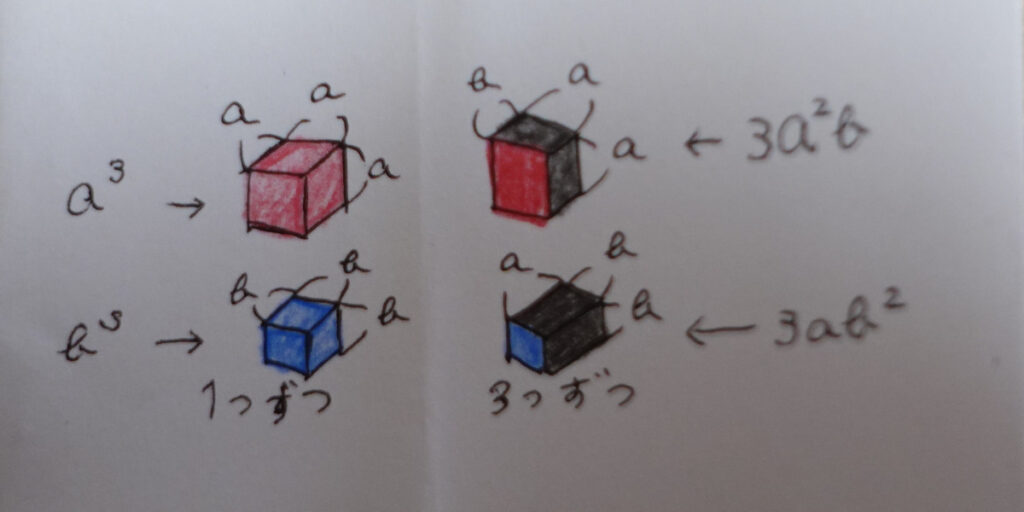
書かれているのは、使用している積み木の構成の説明のようです。
一片の長さがaの立方体(体積はa3)が1個
一片の長さがbの立方体(体積はb3)が1個
縦横の長さがそれぞれa、高さがbの直方体(体積はa2b)が3個
縦横の長さがそれぞれb、高さがaの直方体(体積はab2)が3個
の積み木が使われているとの説明に見えます。
これを見て、私はハタと気が付きました。まさか!
突然ですが、算数と数学の復習です。
- 直方体・立方体の体積
まずは、小学校高学年で習う直方体・立方体の体積の求め方です。
立方体はすべての辺の長さが同じ直方体ですから、
直方体の体積 = 縦の長さ × 横の長さ × 高さ
立方体の体積 = 1辺の長さ × 1辺の長さ × 1辺の長さ
でしたね。
では、1辺の長さが(a+b)の立方体の体積は?
そうです(a+b)3です。 - 3乗の項を含む式の因数分解と展開
次は、いきなり大学受験レベルの数学の話です。
嫌いな人も多い因数分解に以下のような公式があります。
(a+b)3 = a3 + 3a2b + 3ab2 + b3
見るのが嫌になりそうな式ですが、このブログをもう一度眺めてみて何か気づきませんか?
この式の左側と右側の各項がここまでのストーリーに既に出てきていますよね?
そうなんです。
上の②の式で、
左辺の(a+b)3 は、1辺の長さが(a+b)の立方体の体積を表しています。
右辺の a3 + 3a2b + 3ab2 + b3は、今回話題にしている玩具の中の立方体に詰まっている積み木の構成と合致しています。
つまり、この玩具は大学受験レベルの因数分解・展開の公式である
(a+b)3 = a3 + 3a2b + 3ab2 + b3
を、立方体と中に詰まっている積み木を使用して、小学校高学年でも理解できるように可視化したものだったんです。
おそらくこの玩具の作者の意図としては、以下のようなものを子供たちに学んでほしかったのではないかと勝手に想像します。
- 幼い子供に手遊びの中で「立体」に触れてほしかった
- 大きなものは小さなものに分解することができること
- 逆に小さなパーツを組み合わせて大きなものを作り出せること
- 立方体に触れること
- (a+b)3 = a3 + 3a2b + 3ab2 + b3の公式を知った時に、
この玩具の中の積み木の構成を思い起こせること - 幼いころからの遊びで得た経験を学習に結び付けて覚えること
- 難しい内容も、別の観点から可視化できること
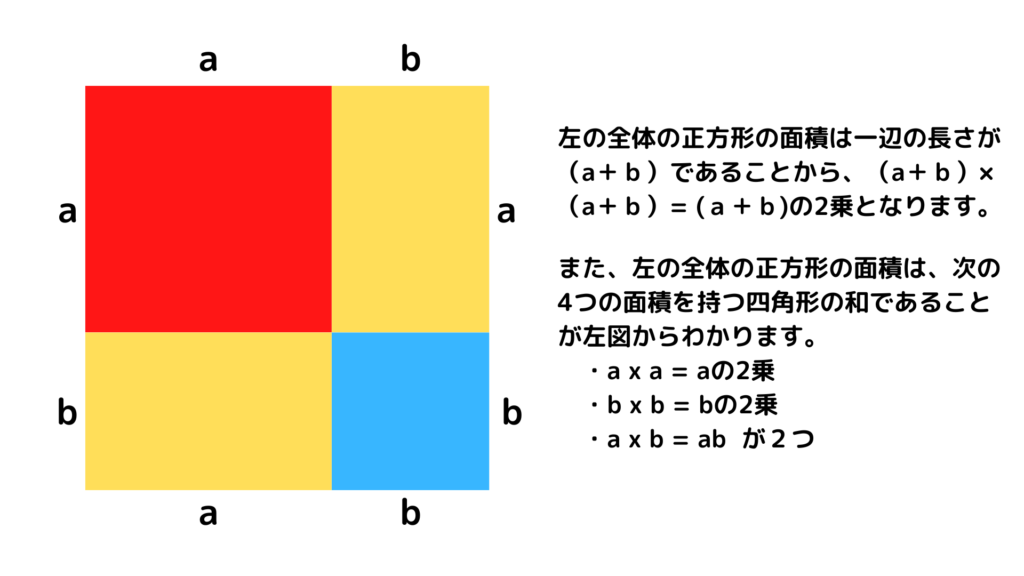
ちなみに、知っている方も多いと思われる2乗の項を含む因数分解・展開の式
(a+b)2 = a2 + 2ab + b2
を可視化して、正方形の面積から説明したものを以下に載せておきます。これは学校でも見た記憶があるかもしれませんね。
実は今回話題にした玩具は、子供が大変お世話になった幼稚園卒園時に卒園記念としていただいたものでした。卒園後、小学校入学を機に他の玩具とともに納戸の隅に押し込められたままになっていたものです。ほんとうにゴメンナサイ。
幼稚園は幼保園であったため子供が小さなころからお世話になり、オシメからトイレ、箸の使い方、お茶の入れ方などの基本的なしつけは同幼保園で身についたといっても過言ではありませんでした。
今回この卒園記念の玩具を今になって認識したことで、あらためて感謝の気持ちでいっぱいになりました。子供には小さなころから多くの方に支えてもらったこと、お世話になったことに感謝することを忘れず、他人から感謝されるような人間になるよう日々成長を続けて欲しいと思います。
以上



